Week 4 - Machine Learning
Non-Linear Hypotheses, Neural Network Model, Multiclass Classification, Regulation

Non-linear Hypotheses
If create a hypothesis with r polynominal terms from $n$ features, then there will be $\frac{(n+r-1)!}{r!(n-1)!}$. For quadratic terms, the time complexity is $O(n^{2}/2)$. Not pratical to compute.
Neural networks offers an alternate way to perform machine learning when we have complex hypotheses with many features.
Neurons and the Brain
There is evidence that the brain uses only one “learning algorithm” for all its different functions. Scientists have tried cutting (in an animal brain) the connection between the ears and the auditory cortex and rewiring the optical nerve with the auditory cortex to find that the auditory cortex literally learns to see.
This principle is called “neuroplasticity” and has many examples and experimental evidence.
Model Representation
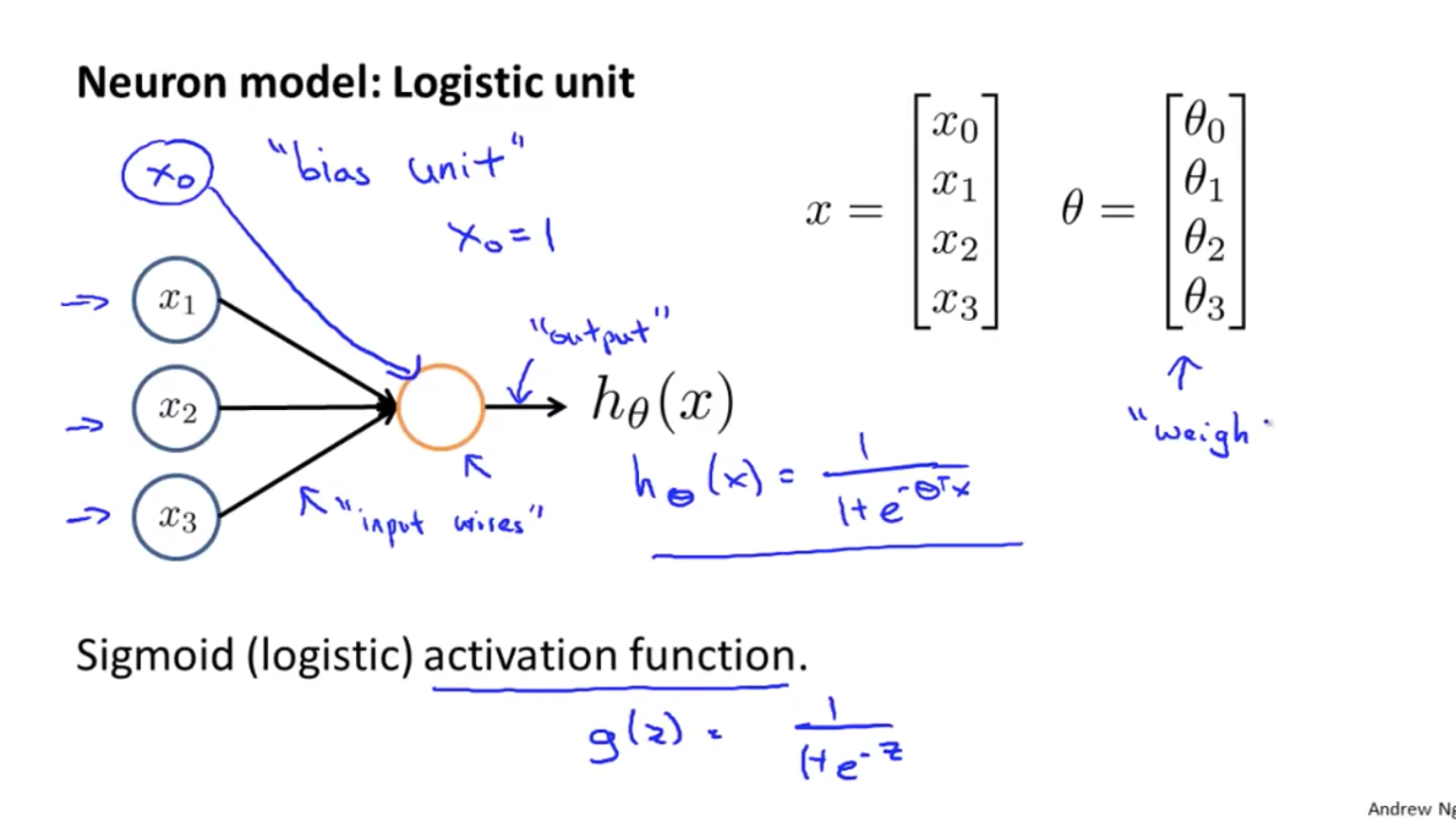
At a very simple level, neurons are basically computational units that take input (dendrites) as electrical input (called “spikes”) that are channeled to outputs (axons).
In our model, our dendrites are like the input features x1⋯xn, and the output is the result of our hypothesis function:
In this model our x0 input node is sometimes called the bias unit. It is always equal to 1.
Our “theta” parameters are sometimes instead called “weights” in the neural networks model.
Activation function is the smae logistic function.
We can have intermediate layers of nodes between the input and output layers called the “hidden layer”.
$$ \begin{align} & a_i^{(j)} = \text{“activation” of unit $i$ in layer $j$} \newline & \Theta^{(j)} = \text{matrix of weights controlling function mapping from layer $j$ to layer $j+1$} \end{align} $$
For example, one hidden layer neural network:
$$ \begin{bmatrix}x_0 \newline x_1 \newline x_2 \newline x_3\end{bmatrix} \rightarrow \begin{bmatrix}a_1^{(2)} \newline a_2^{(2)} \newline a_3^{(2)} \newline \end{bmatrix} \rightarrow h_\theta(x) \begin{align} h_\Theta(x) = a_1^{(3)} = g(\Theta_{10}^{(2)}a_0^{(2)} + \Theta_{11}^{(2)}a_1^{(2)} + \Theta_{12}^{(2)}a_2^{(2)} + \Theta_{13}^{(2)}a_3^{(2)}) \newline a_1^{(2)} = g(\Theta_{10}^{(1)}x_0 + \Theta_{11}^{(1)}x_1 + \Theta_{12}^{(1)}x_2 + \Theta_{13}^{(1)}x_3) \newline a_2^{(2)} = g(\Theta_{20}^{(1)}x_0 + \Theta_{21}^{(1)}x_1 + \Theta_{22}^{(1)}x_2 + \Theta_{23}^{(1)}x_3) \newline a_3^{(2)} = g(\Theta_{30}^{(1)}x_0 + \Theta_{31}^{(1)}x_1 + \Theta_{32}^{(1)}x_2 + \Theta_{33}^{(1)}x_3) \newline \end{align} $$
The dimensions of these matrices of weights is determined as follows:
$\text{If network has $s_j$ units in layer $j$ and $s_{j+1}$ units in layer $j+1$, then $\Theta^{(j)}$ will be of dimension $s_{j+1} \times (s_j + 1)$.}$
Actication Functions
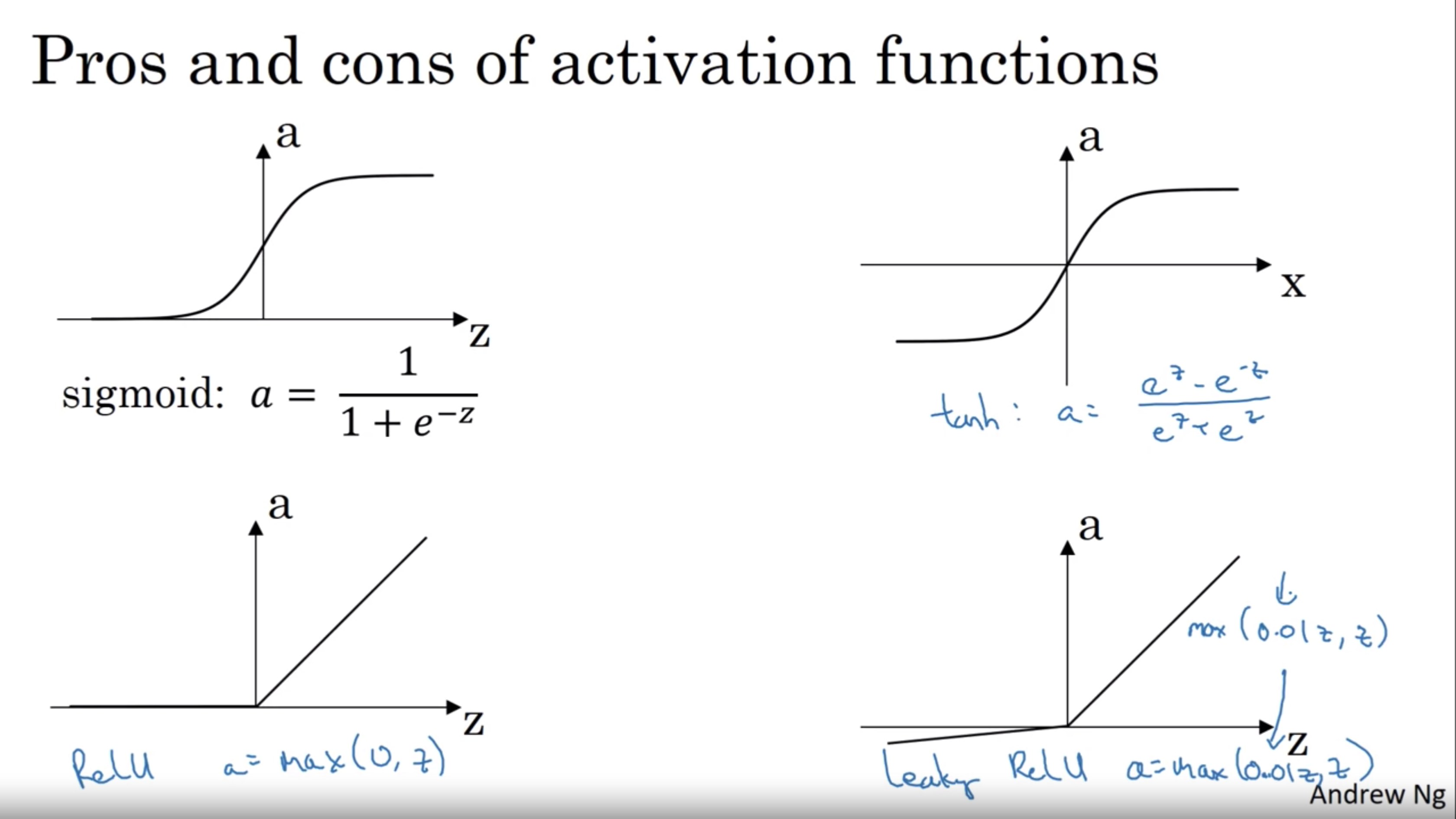
In the deep learning course provided by deeplearning.ai, sigmoid function is not the only activation function in neural network. Most of the time for hidden units, tanh function performs better than sigmoid function because the values between plus 1 and minus 1, the mean of the activations that come out of your head, and they are closer to having a 0 mean. It kind of has the effect of centering your data so that the mean of your data is closer to 0 rather than, maybe 0.5. And this actually makes learning for the next layer a little bit easier.
While, for the output layer of the binary classification, use the sigmoid function. Other than that, tanh function is always a superior choice.
ReLU is rectifier activation function, and the leaky ReLU: https://en.wikipedia.org/wiki/Rectifier_(neural_networks)
Examples and Intuition Ⅰ
$x_1 \text{ AND } x_2$ is the logical ‘and’ operator and is only true if both $x_1$ and $x_2$ are 1.
The graph of our functions will look like:
$$ \begin{align} \begin{bmatrix} x_0 \newline x_1 \newline x_2 \end{bmatrix} \rightarrow \begin{bmatrix} g(z^{(2)}) \end{bmatrix} \rightarrow h_\Theta(x) \end{align} $$
Note $x_0$ is the bias variable and is always 1.
The first layer thata matrix:
$$ \Theta^{(1)} = \begin{bmatrix}-30 & 20 & 20\end{bmatrix} $$
Therefore:
$$ \begin{align} & h_\Theta(x) = g(-30 + 20x_1 + 20x_2) \newline \newline & x_1 = 0 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-30) \approx 0 \newline & x_1 = 0 \ \ and \ \ x_2 = 1 \ \ then \ \ g(-10) \approx 0 \newline & x_1 = 1 \ \ and \ \ x_2 = 0 \ \ then \ \ g(-10) \approx 0 \newline & x_1 = 1 \ \ and \ \ x_2 = 1 \ \ then \ \ g(10) \approx 1 \end{align} $$
Examples and Intuition Ⅱ
The $\theta$ matrices for AND, NOR, and OR are:
$$ \begin{align} AND:\newline \Theta^{(1)} &= \begin{bmatrix}-30 & 20 & 20\end{bmatrix} \newline NOR:\newline \Theta^{(1)} &= \begin{bmatrix}10 & -20 & -20\end{bmatrix} \newline OR:\newline\Theta^{(1)} &= \begin{bmatrix}-10 & 20 & 20\end{bmatrix} \newline \end{align} $$
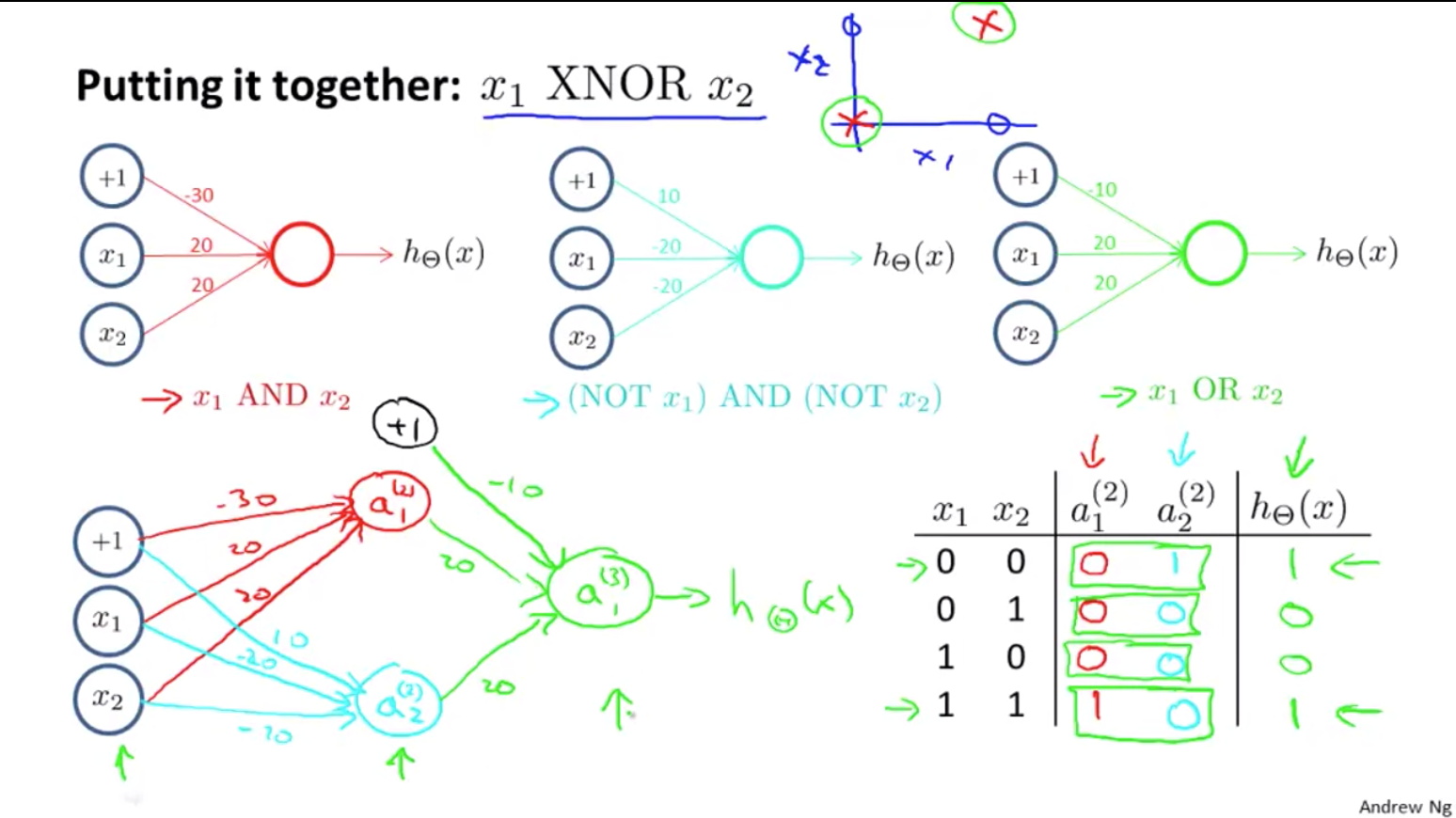
We can combine these to get the XNOR logical operator (which gives 1 if $x_1$ and $x_2$ are both 0 or both 1).
$$ \begin{align} \begin{bmatrix} x_0 \newline x_1 \newline x_2 \end{bmatrix} \rightarrow \begin{bmatrix} a_1^{(2)} \newline a_2^{(2)} \end{bmatrix} \rightarrow \begin{bmatrix} a^{(3)} \end{bmatrix} \rightarrow h_\Theta(x) \end{align} $$ $$ \Theta^{(1)} = \begin{bmatrix} -30 & 20 & 20 \newline 10 & -20 & -20 \end{bmatrix} $$ $$ \Theta^{(2)} = \begin{bmatrix} -10 & 20 & 20 \end{bmatrix} $$
The value for all nodes: $$ \begin{align} & a^{(2)} = g(\Theta^{(1)} \cdot x) \newline & a^{(3)} = g(\Theta^{(2)} \cdot a^{(2)}) \newline & h_\Theta(x) = a^{(3)} \end{align} $$
Multiclass Classification
If we want to classify our data into four final resulting classes, (for example classificate the image to cat, dog, bird, or people):
$$ \begin{align} \begin{bmatrix} x_0 \newline x_1 \newline x_2 \newline \cdots \newline x_n \end{bmatrix} \rightarrow \begin{bmatrix} a_0^{(2)} \newline a_1^{(2)} \newline a_2^{(2)} \newline \cdots \end{bmatrix} \rightarrow \begin{bmatrix} a_0^{(3)} \newline a_1^{(3)} \newline a_2^{(3)} \newline \cdots \end{bmatrix} \rightarrow \cdots \rightarrow \begin{bmatrix} h_\Theta(x)_1 \newline h_\Theta(x)_2 \newline h_\Theta(x)_3 \newline h_\Theta(x)_4 \newline \end{bmatrix} \rightarrow \end{align} $$
Then, our resulting hypothesis for one set of inputs looks like: $$ h_\Theta(x) = \begin{bmatrix} 0 \newline 0 \newline 1 \newline 0 \newline \end{bmatrix} $$